Python dictionaries are an extremely important part of Python. Of course they are important because programmers use them a lot, but that's not the only reason. Another reason is that the interpreter uses them internally to run Python code. CPython does a dictionary lookup every time you access an object attribute or a class variable, and accessing a global or built-in variable also involves a dictionary lookup if the result is not cached. What makes a dictionary appealing is that lookups and other dictionary operations are fast and that they remain fast even as we add more and more elements to the dictionary. You probably know why this is the case: Python dictionaries are hash tables. A hash table is a fundamental data structure. The idea behind it is very simple and widely known. Yet, implementing a practical hash table is not a trivial task. There are different hash table designs that vary in complexity and performance. And new, better designs are constantly being developed.
The goal of this post is to learn how CPython implements hash tables. But understanding all the aspects of hash table design can be hard, and CPython's implementation is especially sophisticated, so we'll approach this topic gradually. In the first part of this post, we'll design a simple fully-functional hash table, discuss its capabilities and limitations and outline a general approach to design a hash table that works well in practice. In the second part, we'll focus on the specifics of CPython's implementation and finally see how Python dictionaries work behind the scenes.
Note: In this post I'm referring to CPython 3.9. Some implementation details will certainly change as CPython evolves. I'll try to keep track of important changes and add update notes.
What is a dictionary
Let us first clarify that a dictionary and a hash table are not the same thing. A dictionary (also known as a map or associative array) is an interface that maintains a collection of (key, value) pairs and supports at least three operations:
- Insert a (key, value) pair:
d[key] = value. - Look up the value for a given key:
d[key]. - Delete the key and the associated value:
del d[key].
A hash table is a data structure that is commonly used to implement dictionaries. We can, however, use other data structures to implement dictionaries as well. For example, we can store the (key, value) pairs in a linked list and do a linear search to look them up. A dictionary can also be implemented as a sorted array or as a search tree. Any of these data structures will do the job. The difference between them is that they have different performance characteristics. Hash tables are a popular choice because they exhibit excellent average-case performance. To see what it means, let's discuss how hash tables work.
Designing a simple hash table
In its essence, a hash table is an array of (key, value) pairs. A nice fact about arrays is that we can access the i-th element of an array in constant time. The main idea of a hash table is to map each key to an array index and then use this index to quickly locate the corresponding (key, value) pair.
Each position in a hash table is called a bucket. Instead of speaking about the mapping between keys and indices, we often speak about the mapping between keys and buckets. A function that maps keys to buckets is called a hash function. Generally speaking, a hash function is any function that maps arbitrary-size data to fixed-size values, so you may hear this term in other contexts as well. We now show one simple way to construct a hash function for hash tables.
To map (or hash) integer keys, we use a hash function of the form h(key) = key % number_of_buckets. It gives the values in the range [0, number_of_buckets - 1]. And this is exactly what we need! To hash other data types, we first convert them to integers. For example, we can convert a string to an integer if we interpret the characters of the string as digits in a certain base. So the integer value of a string of length \(n\) is calculated like this:
where \(base\) is the size of the alphabet.
With this approach, different keys may map to the same bucket. In fact, if the number of possible keys is larger than the number of buckets, then some key will always map to the same bucket no matter what hash function we choose. So we have to find a way to handle hash collisions. One popular method to do that is called chaining. The idea of chaining is to associate an additional data structure with each bucket and store all the items that hash to the same bucket in that data structure. The following picture shows a hash table that uses linked lists for chaining:
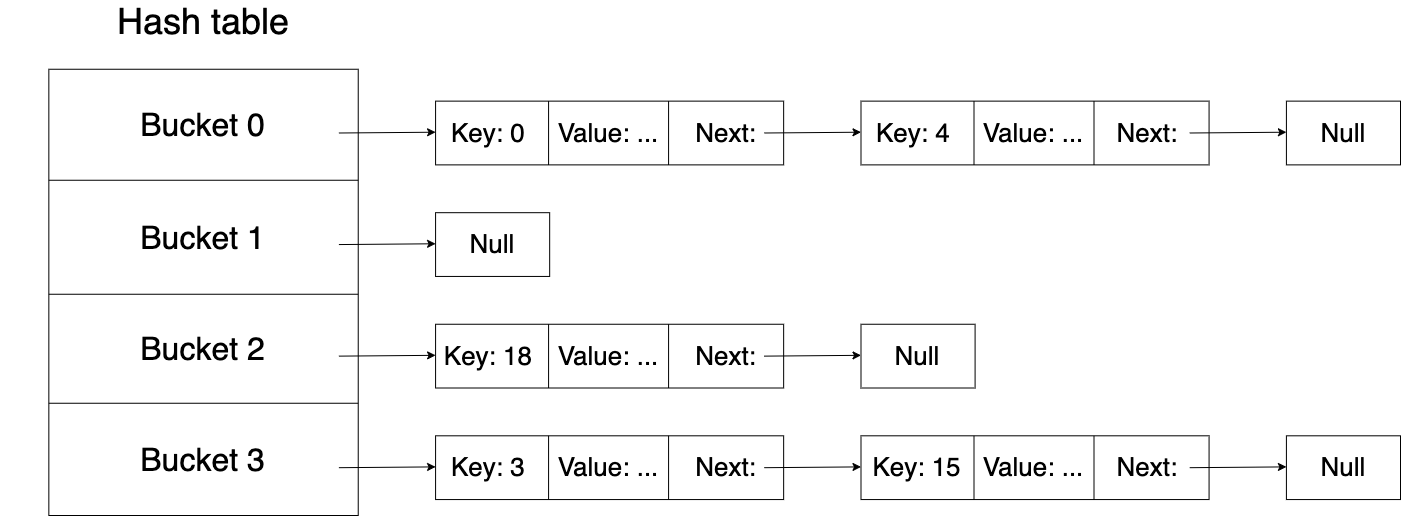
To insert a (key, value) pair into such a table, we first hash the key to get its bucket and then search for the key in the corresponding linked list. If we find the key, we update the value. If we don't find the key, we add a new entry to the list. The lookup and delete operations are done in a similar manner.
Since the comparison of keys may take a long time (e.g. the keys are long strings), the hashes are typically compared first. If the hashes are not equal, then the keys are not equal either. It's a common practice to store hashes along with keys and values to avoid recomputing them each time.
We now have a working hash table. How well does it perform? The worst-case analysis is quite simple. If the set of possible keys is sufficiently large, then there is a non-zero chance that all the items inserted into the hash table happen to be in the same bucket. The average-case performance is more promising. It largely depends on two factors. First, it depends on how evenly the hash function distributes the keys among buckets. Second, it depends on the average number of items per bucket. This latter characteristic of a hash table is called a load factor:
Theory says that if every key is equally likely to hash to any bucket, independently of other keys, and if the load factor is bounded by a constant, then the expected time of a single insert, lookup and delete operation is \(O(1)\).
To see why this statement is true, insert \(n\) different keys into a hash table with \(m\) buckets and calculate the expected length of any chain. It will be equal to the load factor:
For more elaborate proofs, consult a textbook. Introduction to Algorithms (a.k.a. CLRS) is a good choice.
How reasonable are the assumptions of the statement? The load factor assumption is easy to satisfy. We just double the size of the hash table when the load factor exceeds some predefined limit. Let this limit be 2. Then, if upon insertion the load factor becomes more than 2, we allocate a new hash table that has twice as many buckets as the current one and reinsert all the items into it. This way, no matter how many items we insert, the load factor is always kept between 1 and 2. The cost of resizing the hash table is proportional to the number of items in it, so inserts that trigger resizing are expensive. Nevertheless, such inserts are rare because the size of the hash table grows in geometric progression. The expected time of a single insert remains \(O(1)\).
The other assumption means that the probability of a key being mapped to a bucket must be the same for all buckets and equal to 1/number_of_buckets. In other words, the hash function must produce uniformly distributed hashes. It's not that easy to construct such a hash function because the distribution of hashes may depend on the distribution of keys. For example, if the keys are integers, and each integer is equally likely to be the next key, then the modulo hash function h(key) = key % number_of_buckets will give uniform distribution of hashes. But suppose that the keys are limited to even integers. Then, if the number of buckets is even, the modulo hash function will never map a key to an odd bucket. At least half of the buckets won't be used.
It's quite easy to choose a bad hash function. In the next section we'll discuss how to choose a good one.
Hash functions
If we cannot predict what the keys in every possible application will be, then we need to choose a hash function that is expected to uniformly distribute any set of keys. The way to do this is to generate the hash function randomly. That is, with equal probability, we assign a random hash to each possible key. Note that the hash function itself must be deterministic. Only the generation step is random.
In theory, a randomly generated hash function is the best hash function. Unfortunately, it's impractical. The only way to represent such a function in a program is to store it explicitly as a table of (key, hash) pairs, like so:
| key | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|---|---|
| h(key) | 43 | 521 | 883 | 118 | 302 | 91 | 339 | 16 | ... |
And this requires too much memory.
The best thing we can do in practice is to choose a hash function that approximates a randomly generated hash function. There exists a number of approaches to do that. Before we delve into them, note that there is no need to choose a separate hash function for each possible hash table size. What real-world hash tables do instead is introduce an auxiliary hash function that maps keys to fixed-size integers, such as 32-bit or 64-bit ints, and another function that maps these integers to hash table buckets. Only the latter function changes when the size of the hash table changes. Typically, this function is just the modulo operation, so that the bucket for a given key is calculated as follows:
hash(key) % number_of_buckets
It's a common practice to use powers of 2 as the hash table size because in this case the modulo operation can be computed very efficiently. To compute hash(key) % (2 ** m), we just take m lower bits of hash(key):
hash(key) & (2 ** m - 1)
This approach may lead to many hash collisions if the hashes differ mainly in higher bits. To make this situation unlikely, the hash() function should be designed to give a close-to-uniform distribution of hashes.
Some hash table designers do not construct the hash() function properly and resort to certain tricks instead. A common advice is to use prime numbers as the hash table size, so that the bucket for a given key is calculated as follows:
hash(key) % prime_number
Composite numbers are considered to be a bad choice because of this identity:
It means that if a key shares a common factor with the number of buckets, then the key will be mapped to a bucket that is a multiple of this factor. So the buckets will be filled disproportionately if such keys dominate. Prime numbers are recommended because they are more likely to break patterns in the input data.
Another trick is to use powers of 2 as the hash table size but scramble the bits of a hash before taking the modulus. You may find such a trick in the Java HashMap:
/**
* Computes key.hashCode() and spreads (XORs) higher bits of hash
* to lower. Because the table uses power-of-two masking, sets of
* hashes that vary only in bits above the current mask will
* always collide. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward. There is a tradeoff between speed, utility, and
* quality of bit-spreading. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading), and because we use trees to handle large sets of
* collisions in bins, we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage, as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds.
*/
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
No tricks are needed if we choose a proper hash function in the first place. As we've already said, there exists a number of approaches to do that. Let us now see what they are.
Non-cryptographic hash functions
The first approach is to choose a well-known non-cryptographic hash function that was designed for hash tables. The list of such functions includes Jenkins hash, FNV hash, MurmurHash, CityHash, xxHash and many others. These functions take byte sequences as their inputs, so they can be used to hash all kinds of data. To get a rough idea of how they work, let's take a look at the FNV-1a hash. Here's what its Python implementation may look like:
OFFSET_BASIS = 2166136261
FNV_PRIME = 16777619
HASH_SIZE = 2 ** 32
def fvn1a(data: bytes) -> int:
h = OFFSET_BASIS
for byte in data:
h = h ^ byte
h = (h * FNV_PRIME) % HASH_SIZE
return h
For each byte in the input, the function performs two steps:
- combines the byte with the current hash value (xor); and
- mixes the current hash value (multiplication).
Other hash functions have this structure too. To get an idea of why they work that way and why they use particular operations and constants, check out Bret Mulveyʼs excellent article on hash functions. Bret also explains how to evaluate the quality of a hash function, so we won't discuss it here. Some very interesting results can be found in this answer on StackExchange. Check them out too!
A fixed non-cryptographic hash function performs well in practice under normal circumstances. It performs very poorly when someone intentionally tries to supply bad inputs to the hash table. The reason is that a non-cryptographic hash function is not collision-resistant, so it's fairly easy to come up with a sequence of distinct keys that all have the same hash and thus map to the same bucket. If a malicious user inserts a sequence of \(n\) such keys, then the hash table will handle the input in \(O(n^2)\). This may take a long time and freeze the program. Such an attack is known as a Hash DoS attack or hash flooding. A potential target of hash flooding is a web application that automatically parses incoming query parameters or POST data into a dictionary. Since most web frameworks offer this functionality, the problem is real. Next we'll look at two approaches to choose a hash function that solve it.
Universal hashing
Note that attackers won't be able to come up with a sequence of colliding keys if they know nothing about the hash function used. So a randomly generated hash function is again the best solution. We said that we cannot use it in practice because it cannot be computed efficiently. But what if we randomly choose a hash function from a family of "good" functions that can be computed efficiently, won't it do the job? It will, though we need to find a suitable family of functions. A family won't be suitable, for example, if we can come up with a sequence of keys that collide for every function in the family. Ideally, we would like to have a family such that, for any set of keys, a function randomly chosen from the family is expected to distribute the keys uniformly among buckets. Such families exist, and they are called universal families. We say that a family of functions is universal if, for two fixed distinct keys, the probability to choose a function that maps the keys to the same bucket is less than 1/number_of_buckets:
It means that an average function from a universal family is unlikely to produce colliding hashes for two distinct keys.
Just to get an idea of what a universal family may look like, here's a classic example of a universal family for hashing integer keys:
where \(p\) is any fixed prime number at least as large as the number of possible keys, and \(a \in \{1, ...p-1\}\) and \(b \in \{0, ...p-1\}\) are parameters chosen at random that specify a concrete hash function from the family.
What does universality give us? Suppose that we randomly choose a hash function from a universal family and use this hash function to insert a sequence of keys into a hash table with chaining and table resizing as described in the previous section. Then theory says that the expected length of each chain in the hash table is bounded by a constant. This implies that the expected time of a single insert, lookup and delete operation is \(O(1)\). And it does not matter what keys we insert!
Note that we've made a similiar statement before:
Theory says that if every key is equally likely to hash to any bucket, independently of other keys, and if the load factor is bounded by a constant, then the expected time of a single insert, lookup and delete operation is \(O(1)\).
The important difference is that in the case of universal hashing the word "expected" means averaging over hash functions, while the statement from the previous section refers to averaging over keys.
To learn more about the theory behind universal hashing, read the paper by Lawrence Carter and Mark Wegman that introduced this concept. For examples of universal families, see Mikkel Thorup's survey.
Universal hashing looks good in theory because it guarantees excellent average-case performance and protects against hash flooding. Nevertheless, you won't find many hash table implementations that actually use it. The reason is a combination of two facts:
- Universal hash functions are not as fast as the fastest non-universal hash functions.
- Universal hash functions do not protect against advanced types of hash flooding.
What does the second point mean? It is true that if a universal hash function is used, attackers cannot come up with a sequence of colliding keys beforehand. But if the attackers can observe how the hash function maps keys, they may be able to deduce how it works and come up with such a sequence. This situation is possible when users work with the hash table interactively: insert a key, then look up a key, then insert a key again and so on. To learn how the hash function maps keys, the attackers can perform a timing attack. First, they insert a single key into the hash table. Then they try to find some other key that maps to the same bucket. Such a key can be detected using a lookup because if a key maps to the same bucket the lookup takes more time. This is one way in which the information about the hash function may leak. Once it leaks, universal hashing doesn't give us any guarantees.
The described attack is known as advanced hash flooding. It was identified by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012. At that time, most hash table implementations used non-cryptographic hash functions. Some of those hash functions employed an idea of universal hashing and took a randomly generated seed. Still, they were vulnerable to hash flooding. Aumasson and Bernstein pointed out this problem and argued that because of advanced hash flooding, even true universal hashing couldn't be a solution. As a solution, they developed a keyed hash function called SipHash, which is now widely used.
SipHash
SipHash takes a 128-bit secret key and a variable-length input and produces a 64-bit hash. Unlike non-cryptographic hash functions, SipHash is designed to have certain cryptographic properties. Specifically, it's designed to work as a message authentication code (MAC). MACs guarantee that it's not feasible to compute the hash of a given input without knowing the secret key even when the hash of any other input is at hand. Thus, if the secret key is randomly generated and unknown to attackers, SipHash protects against advanced hash flooding.
Note that no hash function including SipHash can prevent the attackers from finding the colliding keys by bruteforce as we've seen in the example of a timing attack. This approach, however, requires \(O(n^2)\) requests to find \(n\) colliding keys, so the potential damage caused by the attack is significantly reduced.
Note also that there is no formal proof of SipHash's security. Such proofs are beyond the state of the art of modern cryptography. Moreover, it's conceivable that someone will break SipHash in the future. Nevertheless, some cryptanalysis and evidence show that SipHash should work as a MAC.
SipHash is not as fast as some non-cryptographic hash functions, but its speed is comparable. The combination of speed and security made SipHash a safe bet for a general-purpose hash table. It's now used as a hash function in Python, Perl, Ruby, Rust, Swift and other languages. To learn more about SipHash, check out the paper by Aumasson and Bernstein.
The choice of the hash function plays a huge role in the performance of a hash table. It is, however, not the only choice hash table designers have to make. They also have to decide how to handle hash collisions. Chaining is one option, but there are other methods that often perform better. In fact, most state-of-the-art hash tables use methods other than chaining. Let us now see what those methods are.
Collision resolution methods
We saw that chaining can be used to implement a hash table whose average-case performance is constant. Asymptotically, we cannot do better. But asymptotic behavior is not what's important in practice. What's important in practice is the actual time it takes to process real-world data and the amount of memory required to do that. From this perspective, other collision resolution methods often perform better than chaining. Most of them are based on the same idea called open addressing.
In open addressing, all items are stored directly in the hash table. Hash collisions are resolved by using a hash function of a special form. Instead of mapping each key to a single bucket, a hash function of this form maps each key to a sequence of buckets. Such a sequence is called a probe sequence. Buckets in a probe sequence are called probes.
To insert a new (key, value) pair in a hash table with open addressing, we iterate over the buckets in the probe sequence until we find an empty bucket and store the key and the value in that bucket. We'll always find an empty bucket eventually if the hash table is not full and if the probe sequence covers all the buckets in the hash table. In addition to that, the probe sequence should be a permutation of buckets since visiting the same bucket more than once is a waste of time. The following picture illustrates the insertion process into a hash table with open addressing:
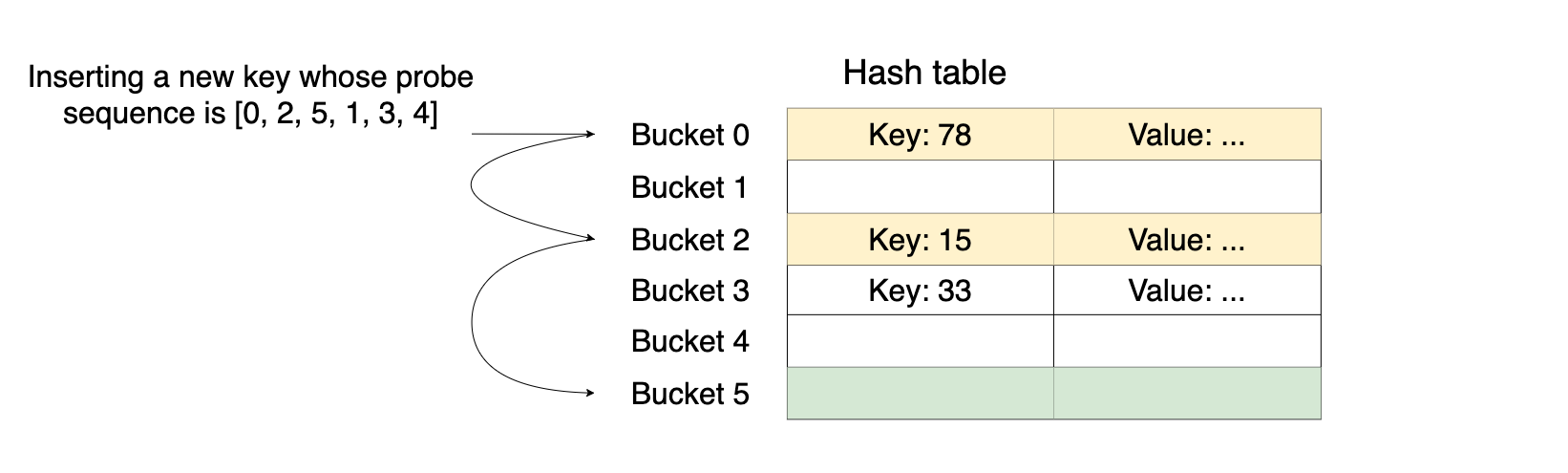
To look up the value of a key, we iterate over the buckets in the probe sequence until we either find the key or find an empty bucket. If we find an empty bucket, then the key is not in the hash table because otherwise it would be inserted into the empty bucket that we found.
Deleting a key from a hash table with open addressing is not that straightforward. If we just clear the bucket that the key occupies, then some lookups will break because lookups assume that probe sequences don't have gaps. This picture illustrates the problem:
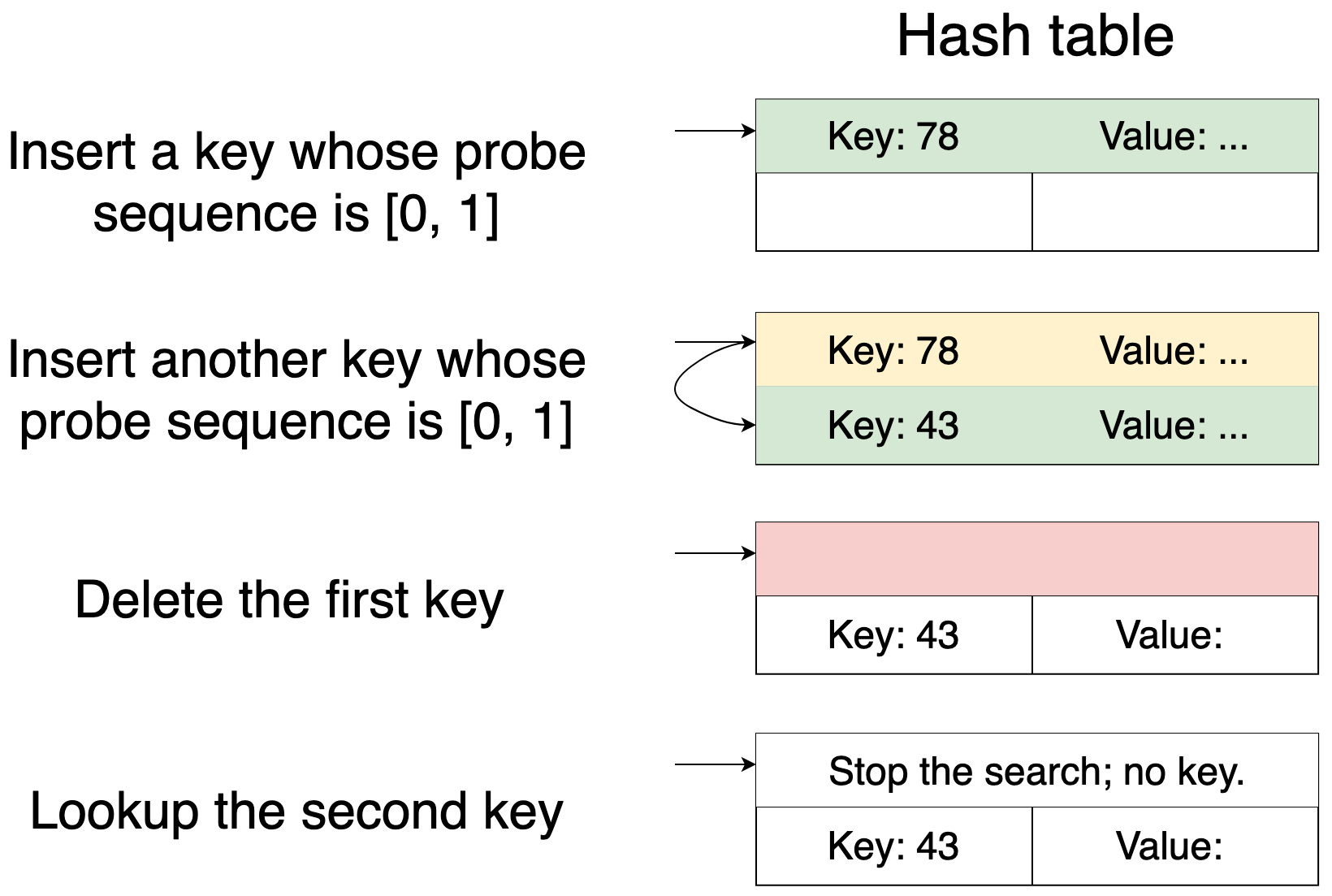
The problem is typically solved by marking the item deleted instead of actually deleting it. This way, it continues to occupy the bucket, so lookups do not break. A deleted item goes away completely in one of two ways. It's either displaced by a new item or removed when the hash table resizes.
One advantage of open addressing over chaining is that the hash table doesn't store a linked list pointer for every item in the hash table. This saves space. On the other hand, empty buckets take more space because each bucket stores an item instead of a pointer. Whether a hash table with open addressing is more memory-efficient depends on the size of items. If the items are much larger than pointers, then chaining is better. But if the items take little space (e.g. the keys and the values are pointers themselves), then open addressing wins. The saved space can then be used to increase the number of buckets. More buckets means less hash collisions, and less hash collisions means the hash table is faster.
So, how do we construct a hash function that returns probe sequences? Typically, it's built of ordinary hash functions that we studied before. In linear probing, for example, an ordinary hash function is used to compute the first probe. Every next probe is just the next bucket in the hash table:
probes[i] = hash(key) + i % number_of_buckets
So if the first probe is bucket b, then the probe sequence is:
[b, b + 1, b + 2, ..., number_of_buckets - 1, 0, 1, ..., b - 1]
Despite its simplicity, linear probing guarantees constant average-case performance under two conditions. The first conditions is that the load factor must be strictly less than 1. The second condition is that the hash() function must map every key with equal probability to any bucket and independently of other keys.
As we've already discussed, the second condition is hard-to-impossible to satisfy. In practice, we choose a hash function that works well enough, but linear probing is very sensitive to the quality of the hash function, so it's harder to do. Another issue is that the load factor must be low if we want a decent performance. Consider the following estimate of the expected number of scanned buckets to insert a new key that Donald Knuth derives in his proof of the statement:
If we take a load factor of 90%, then we'll have about 50 buckets scanned on average assuming that the number of items in the hash table is sufficiently large. Thus, the load factor should be much lower. And that means more empty buckets and higher memory usage.
When we insert a new key or look up a key that is not in a hash table, we want to find an empty bucket as soon as possible. With linear probing it can be a problem because of contiguous clusters of occupied buckets. Such clusters tend to grow because the larger the cluster is, the more likely the next key will hash to a bucket in that cluster and will be inserted at its end. This problem is known as primary clustering.
Quadratic probing solves the primary clustering problem and is less sensitive to the quality of the hash function. It's similar to linear probing. The difference is that the value of the i-th probe depends quadratically on i:
probes[i] = hash(key) + a * i + b * (i ** 2) % number_of_buckets
The constants a and b must be chosen carefully for the probe sequence to cover all the buckets. When the size of the hash table is a power of 2, setting a = b = 1/2 guarantees that the probe sequence will cover all the buckets before it starts repeating them. What does the probe sequence look like in this case? If the first probe is bucket b, then the sequence goes like b, b + 1, b + 3, b + 6, b + 10, b + 15, b + 21 and so on (modulo number_of_buckets). Note that the intervals between consecutive probes increase by 1 at each step. This is a well-known sequence of triangular numbers, and triangular numbers are guaranteed to produce complete probe sequences. See this paper for the proof.
An alternative to quadratic probing is pseudo-random probing. Like other probing schemes, it calls an ordinary hash function to compute the first probe:
probes[0] = hash(key) % number_of_buckets
Then it passes the first probe as a seed to a pseudo-random number generator (PRNG) to compute the subsequent probes. Typically, the PRNG is implemented as a linear congruential generator, so the probes are computed as follows:
probes[i] = a * probes[i-1] + c % number_of_buckets
Hull–Dobell Theorem tells us how to choose the constants a and c so that the probe sequence covers all the buckets before it starts repeating them. If the size of the hash table is a power of 2, then setting a = 5 and c = 1 will do the job.
Quadratic probing and pseudo-random probing are still quite sensitive to the quality of the hash function because the probe sequences of two different keys will be identical whenever their first probes are the same. This situation is also a form of clustering known as secondary clustering. There is a probing scheme that mitigates it. It's called double hashing.
In double hashing, the interval between two consecutive probes depends on the key itself. More specifically, a second, independent hash function determines the interval, so the probe sequence is calculated as follows:
probes[i] = hash1(key) + hash2(key) * i % number_of_buckets
To ensure that the probe sequence covers all the buckets, the hash2() function must produce hashes that are relatively prime to the number of buckets, that is, hash2(key) and number_of_buckets must have no common factors except 1. This can be achieved by constructing the hash2() function in such a way so that it always returns an odd number and by setting the size of the hash table to a power of 2.
The more "random" probe sequences are, the less likely clustering is to occur and the less probes are needed. Thus, in theory, such sequences are better. But theory and practice do not always agree. Up until now we've been measuring the time complexity of algorithms in the number of elementary steps, such as the number of probes or the number of traversed linked list nodes. This metric works fine for asymptotic analysis, but it does not agree with the actual time measurements because it assumes that the cost of each elementary step is roughly the same, and that's not true in reality. In reality, the steps that access main memory are the most expensive. A single access to RAM takes about 100 ns. Compare it to the cost of accessing the fastest CPU cache – it's about 1 ns. Therefore, one of the most important aspects of hash table design is the effective use of the cache.
Linear probing may perform quite well because it's very cache-friendly. To see why, recall that data is moved from the main memory to the cache in cache lines, which are contiguous blocks of memory, typically 64 bytes long. When the contents of the first bucket in a probe sequence have been read, the contents of the next several buckets are already in the cache.
As a general rule, a data structure will be more cache-effective if the items that are often used together are placed close to each other in memory. Linear probing follows this rule much better than other probing schemes. And open addressing in general works better than chaining in this respect because in chaining each item sits in a separately allocated node.
To better comprehend how much the cache affects hash table performance, consider the following graph:
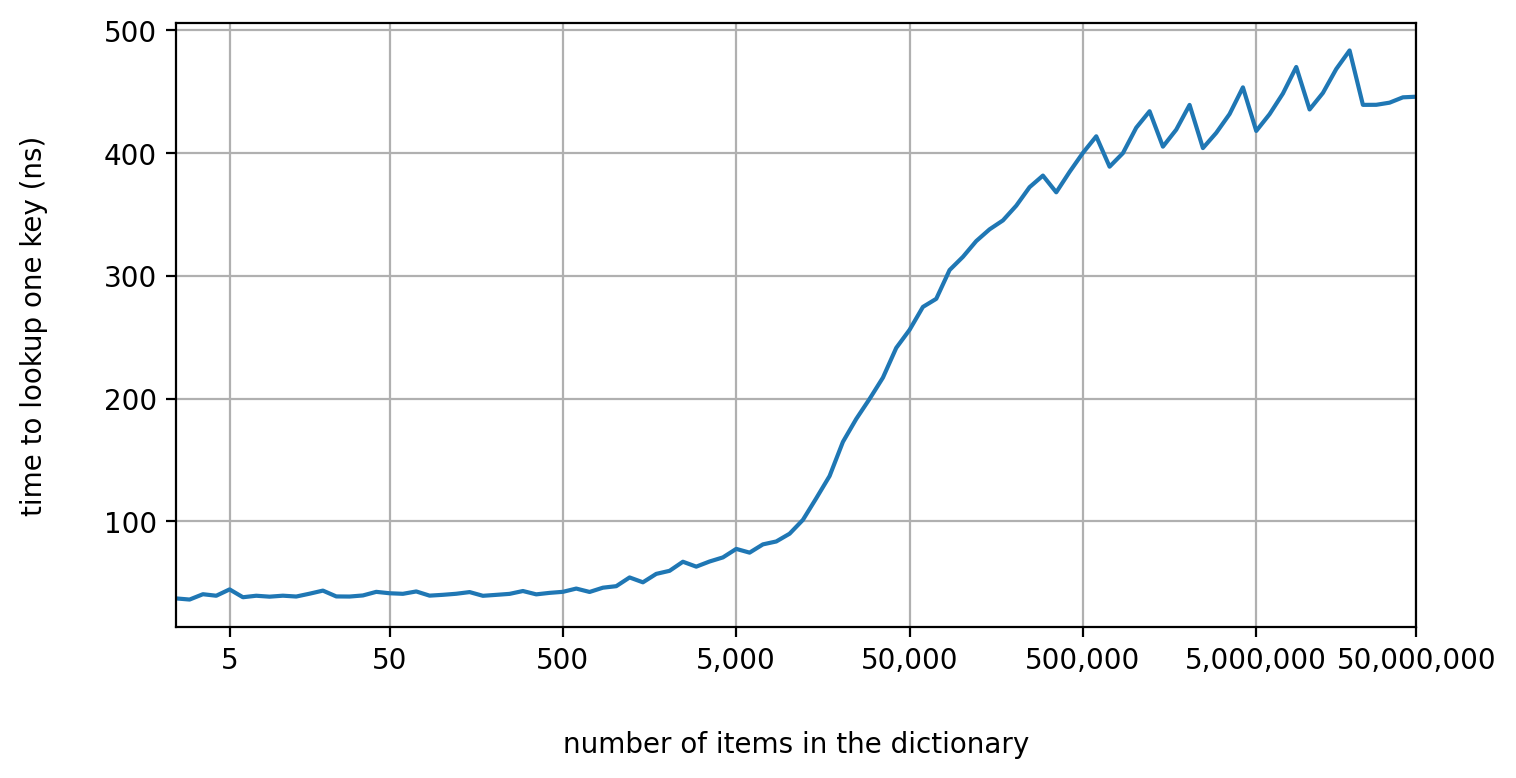
This graph shows how the time of a single lookup in a Python dictionary changes as the number of items in the dictionary increases. It is clear that the time is not constant but increases as well. Why? Hash collisions are not the reason because the keys were chosen at random from a uniform distribution. You might also think that it's a peculiarity of a Python dictionary, but it's not. Any other hash table would behave similarly. The real reason is that when the hash table is small, it fits completely into the cache, so the CPU doesn't need to access the main memory. As the hash table grows larger, the portion of the hash table that is not in the cache grows as well, and the CPU has to access the main memory more frequently.
By the way, have you noticed those zigzags in the graph? They indicate the moments when the hash table resizes.
We discussed a number of methods to resolve hash collisions: chaining and open addressing with various probing schemes. You probably think, "Why do we need all of them?" The reason is that different methods suit different use cases. Chaining makes sense when the items are large and when deletes are frequent. Linear probing works best when the items are small and when the hash function distributes the keys uniformly. And quadratic probing, pseudo-random probing and double hashing are a safe bet in most cases.
State-of-the-art hash tables are typically variations of open addressing with some improvements. Google's Swiss Table, for example, uses SIMD instructions to probe several buckets in parallel. This talk explains how it works in detail. Robin Hood hashing is perhaps the most popular advanced method to resolve hash collisions. To understand the idea behind it, observe that the number of probes to look up a key equals the number of probes that was required to insert it. Naturally, we would like to keep those numbers low. And that's what Robin Hood hashing tries to do. When a new key gets inserted, it doesn't just wait for an empty bucket but can also displace other keys. It displaces any key whose final probe number is less than the number of the current probe. The displaced key then continues on its probe sequence, possibly displacing other keys. As a result, large probe numbers do not emerge, and lookups become faster. To learn more about the benefits of Robin Hood hashing, check out this post. See also Malte Skarupke's talk for an overview of advanced methods to resolve hash collisions.
Well done! We've covered the essentials of hash table design. There is much more to say on this topic, but we now know enough to understand how Python dictionaries work. Without further ado, let's apply our knowledge.
Python dictionaries
Overview
A Python dictionary is a hash table with open addressing. Its size is always a power of 2 and is initially set to 8. When the load factor exceeds 2/3, the hash table resizes. Usually, the size just doubles, but it can also be set to some lesser power of 2 if deleted items occupy a lot of buckets. In short, the load factor varies between 1/3 and 2/3.
The hash of a Python object is a 32-bit or 64-bit singed integer (on 32-bit and 64-bit platforms respectively). We call the built-in hash() function to compute it, and this function works by calling the tp_hash slot of the object's type. Built-in types implement the tp_hash slot directly, and classes can implement it by defining the __hash__() special method. Thus, the hash function is different for different types. Strings and bytes objects are hashed with SipHash, while other types implement custom, simpler hashing algorithms.
The hash of an integer, for example, is usually the integer itself:
$ python -q
>>> hash(1)
1
>>> hash(2343)
2343
>>> hash(-54)
-54
This is not always the case because Python integers can be arbitrary large. So CPython implements a hashing algorithm that works like this:
MODULUS = 2 ** 61 - 1 # Mersenne prime; taking the modulus is efficient
def hash_unoptimized(integer):
"""Unoptimized version of hash() for integers"""
hash_value = abs(integer) % MODULUS
if integer < 0:
hash_value = -hash_value
if hash_value == -1: # -1 indicates an error; do not use it
return -2
return hash_value
Because the algorithm is so simple, it's very easy to come up with a sequence of integers that all have the same hash:
$ python -q
>>> modulus = 2 ** 61 - 1
>>> hash(0)
0
>>> hash(modulus)
0
>>> hash(modulus * 2)
0
>>> hash(modulus * 3)
0
>>> hash(modulus * 1000)
0
Isn't this a security issue? Apparently, CPython developers thought that nobody in a sane mind would cast keys to integers automatically when parsing untrusted user input, so they decided not to use SipHash in this case.
But even non-malicious inputs exhibit regularities that such a primitive hash function won't break. To mitigate the effects of poorly distributed hashes, CPython implements a clever probing scheme.
The probing scheme is pseudo-random probing with a modification. To see the reasoning behind this modification, recall that pseudo-random probing suffers from secondary clustering: the whole probe sequence is determined by the first probe, and the first probe depends only on lower bits of the hash (m lower bits when the size of the hash table is 2**m). CPython solves this problem by perturbing the first few probes with values that depend on higher bits of the hash. Here's what the algorithm that computes probes looks like:
def get_probes(hash_value, hash_table_size):
mask = hash_table_size - 1 # used to take modulus fast
perturb = hash_value # used to perturb the probe sequence
probe = hash_value & mask
while True:
yield probe
perturb >>= 5
probe = (probe * 5 + perturb + 1) & mask
Initially, perturb is set to the hash value. Then, at each iteration, it is shifted 5 bits to the right and the result is added to the linear congruential generator to perturb the next probe. This way, every next probe depends on 5 extra bits of the hash until perturb becomes 0. When perturb becomes 0, the linear congruential generator is guaranteed to cover all the buckets by the Hull–Dobell Theorem.
Despite the clever probing scheme, CPython's hash tables seem very inefficient. First, their maximum load factor is 2/3, which is about 66.6%, and this is when state-of-the-art hash tables work well with load factors of 90% and more. So there is a huge room for improvement here. Second, pseudo-random probing is not cache-friendly. And we saw how important the cache is.
Are CPython's hash tables really as inefficient as they seem? Well, they certainly perform worse than Google's Swiss Table with hundreds of millions of items. But they are not optimized for such huge loads. They are optimized to be compact and to be fast when the hash table is small enough to fit into the cache. This is because the most important uses of Python dictionaries are the storage and retrieval of object attributes, class methods and global variables. And in this cases, the dictionaries are typically small and many.
CPython employs some interesting optimizations to better fit the use cases above. Let's take a look at them.
Compact dictionaries
Before version 3.6, the layout of CPython's hash tables was typical. Each bucket held a 24-byte entry that consisted of a hash, a key pointer and a value pointer. So the following dictionary:
d = {"one": 1, "two": 2, "three": 3}
would be represented like this:
hash_table = [
('--', '--', '--'),
(542403711206072985, 'two', 2),
('--', '--', '--'),
(4677866115915370763, 'three', 3),
('--', '--', '--'),
(-1182584047114089363, 'one', 1),
('--', '--', '--'),
('--', '--', '--')
]
In CPython 3.6 the layout changed. Since then, the entries are stored in a separate, dense array, and the hash table stores only the indices to that array. The same dictionary is now represented like this:
hash_table = [None, 1, None, 2, None, 0, None, None]
entries = [
(-1182584047114089363, 'one', 1),
(542403711206072985, 'two', 2),
(4677866115915370763, 'three', 3),
('--', '--', '--'),
('--', '--', '--')
]
Each index to the entries array takes 1, 2, 4 or 8 bytes depending on the size of the hash table. In any case it is much less than 24 bytes taken by an entry. As a result, empty buckets take less space, and dictionaries become more compact. Of course, the entries array should have extra space for future entries as well. Otherwise, it would have to resize on every insert. But CPython manages to save space nonetheless by setting the size of the entries array to 2/3 of the size of the hash table and resizing it when the hash table resizes.
This optimization has other benefits too. Iteration over a dictionary became faster because entries are densely packed. And dictionaries became ordered because items are added to the entries array in the insertion order.
Shared keys
CPython stores the attributes of an object in the object's dictionary. Since instances of the same class often have the same attributes, there can be a lot of dictionaries that have the same keys but different values. And that's another opportunity to save space!
Since CPython 3.3, object dictionaries of the same class share keys. The keys and hashes are stored in a separate data structure in the class, and the dictionaries store only a pointer to that structure and the values.
For example, consider a simple class whose instances have the same two attributes:
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
And consider two instances of this class:
p1 = Point(4, 4)
p2 = Point(5, 5)
The dictionaries of p1 and p2 will store their own arrays of values but will share everything else:
hash_table = [None, 1, None, None, 0, None, None, None]
entries = [
(-8001793907708313420, 'x', None),
(308703142051095673, 'y', None),
('--', '--', '--'),
('--', '--', '--'),
('--', '--', '--')
]
values_p1 = [4, 4, None, None, None]
values_p2 = [5, 5, None, None, None]
Of course, the keys can diverge. If we add a new attribute to an object, and this attribute is not among the shared keys, then the object's dictionary will be converted to an ordinary dictionary that doesn't share keys. And the dictionaries of new objects won't share keys as well. The conversion will not happen only when the object is the sole instance of the class. So you should define all the attributes on the first instance before you create other instances. One way to do this is to define the attributes in the __init__() special method.
To learn more about key-sharing dictionaries, check out PEP 412.
String interning
To look up a key in a hash table, CPython has to find an equal key in the probe sequence. If two keys have different hashes, then CPython may safely assume that the keys are not equal. But if the keys have the same hash, it must compare the keys to see if they are equal or not. The comparison of keys may take a long time, but it can be avoided altogether when the keys are in fact the same object. To check whether this is the case, we can just compare their ids (i.e. memory addresses). The only problem is to ensure that we always use the same object.
When we create two strings with the same contents, we often get two equal but distinct objects:
$ python -q
>>> a = 'hi!'
>>> b = 'hi!'
>>> a is b
False
To get a reference to the same object, we need to use the sys.intern() function:
>>> import sys
>>> a = sys.intern('hi!')
>>> b = sys.intern('hi!')
>>> a is b
True
The first call to sys.intern() will return the passed string but before that it will store the string in the dictionary of interned strings. The dictionary will map the string to itself, and the second call will find the string in the dictionary and return it.
CPython interns many strings automatically. For example, it interns some string constants:
>>> a = 'hi'
>>> b = 'hi'
>>> a is b
True
These are all the string constants that match this regex:
[a-zA-Z0-9_]*
CPython also interns the names of variables and attributes so we don't have to do that ourselves.
This concludes our study of Python dictionaries. We discussed the most important ideas behind them but left out some implementation details. If you want to know those details, take a look at the source code in Objects/dictobject.c.
A note on sets
Dictionaries are closely related to sets. In fact, sets are just dictionaries without values. Because of this, you might think that CPython implements sets in the same way as it implements dictionaries. But it doesn't. A set is a different object and the hash table behind it works a bit differently. For example, its maximum load factor is not 66.6% but 60%, and if there are less than 50,000 items in the set, its growth factor is not 2 but 4. The most important difference is in the probing scheme. Sets use the same pseudo-random probing but, for every probe, they also inspect 9 buckets that follow the probe. It's basically a combination of pseudo-random and linear probing.
CPython doesn't rely on sets internally as it relies on dictionaries so there is no need to optimize them for specific use cases. Moreover, the general use cases for sets are different. Here's a comment from the source code that explains this:
Use cases for sets differ considerably from dictionaries where looked-up keys are more likely to be present. In contrast, sets are primarily about membership testing where the presence of an element is not known in advance. Accordingly, the set implementation needs to optimize for both the found and not-found case.
The implementation of sets can be found in Objects/setobject.c.
Conclusion
It's not that hard to implement your own hash table once you've seen how others do it. Still, it is hard to choose a hash table design that fits your use case best. CPython implements hash tables that are optimized both for general and internal use. The result is a unique and clever design. But it is also controversial. For example, the probing scheme is designed to tolerate bad hash functions, and this may come at the expense of cache-friendliness. Of course, it's all talk, and only benchmarks can tell the truth. But we cannot just take some state-of-the-art hash table for C++ and compare it with a Python dictionary because Python objects introduce overhead. A proper benchmark would implement Python dictionaries with different hash table designs. It's a lot of work, though, and I don't know of anyone who did it. So, do you have any plans for the next weekend?
The dict type is a part of the builtins module, so we can always access it. Things that are not in builtins have to be imported before they can be used. And that's why we need the Python import system. Next time we'll see how it works.
If you have any questions, comments or suggestions, feel free to contact me at victor@tenthousandmeters.com